Complex
Function 4D Visuals in Desmos
|
Complex
Function 4D Visuals in Geogebra
|
The following visualisations are Desmos
files, allowing toying with the parameters and
animating the graph.
They are visualisations of complex functions w=f(z),
where z=x+iy and w=u+iv are complex
variables.
The "Info" entries can be opened with the
triangle icons to read information about the topic.
The "Control" entries can be opened with ditto
icons, to find slider controls for changing or animating
variables.
The "Show" entries can be activated by clicking
in the empty circle icons, to visualise the topic items.
|
Another interactive tool at our disposal is Geogebra.
The great advantage of it is its 3D (x,y,z)
graphing capability, with surface texture's coloring and
transparency.
Its editor though is very shaky, with arbitrary
results when trying to select a piece of text or
formula, no control where to put and group your formulas
(it groups and orders them by type, not by one's logical
objects), jumping to its top position after confirming
each edit, accidental delets and saves...
Anyway, it's nice to compare this output with the
previous.
And I'm abiding the epoch when mainstream mathwizz
software will finally discover this "true 4D"
method, and incorporate it in its powerful rendering
libraries.
I've grouped all next examples in this 'public book':
https://www.geogebra.org/m/bmuqbufn
|
A 4D coordinate system in 2D:
Axes x and u coincide originally with the
graph's orthogonal coordinates X and Y, with same units
(°). Axes y and v are projected upon the graph's X,Y
plane, so that the units of the axis pairs x,y and u,v
belong to ellipses which represent projected circles
around the origin. These axis projections are described
by
three values:
the shorter axis (y or v unit; the greater axis=1: x or
u unit): see b and bw;
a tilt angle of the ellips: see d and dw;
a rotation angle of x,y or u,v in their respective
ellips: see j and jw.
(°) The "real plane" (x,u) can be made to
coincide with the graph plane X,Y by changing
the 4D axes controls to the values:
b=d=j=bw=jw=0, and dw=pi/2 (~1.57)
|
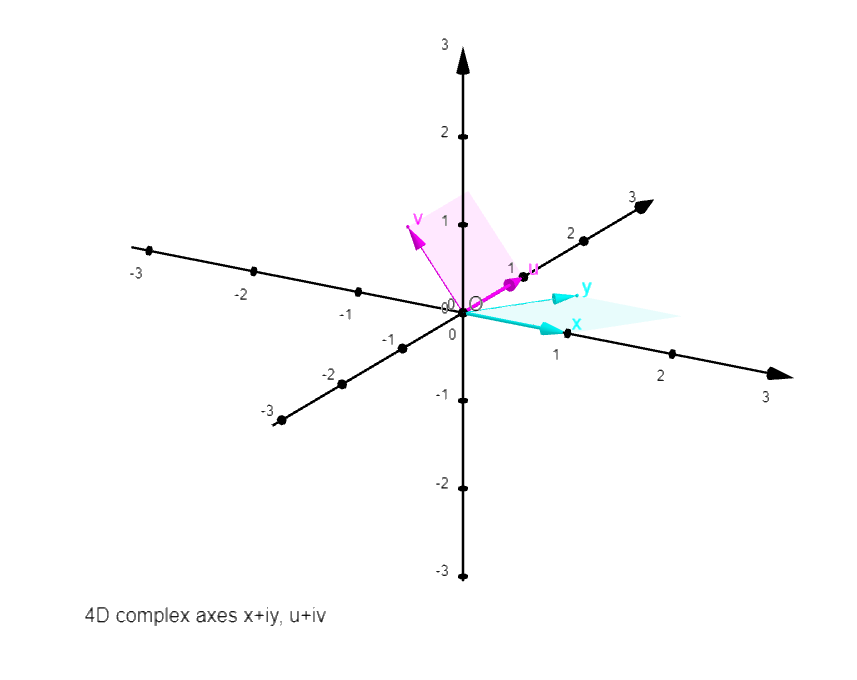
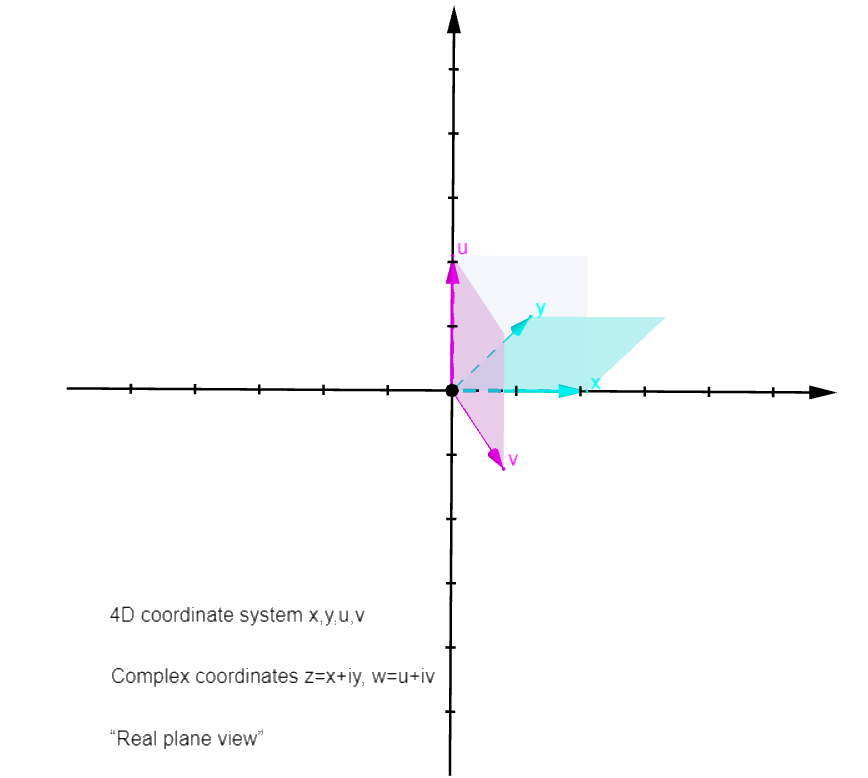
A
4D coordinate system in "3D in 2D":
Axes x and u coincide with the graph's coordinates X and
Y, with same units. Axes y and v are projected upon the
graph's X,Y,Z space, along unit vectors determined by
two angles each:
b_y and b_v = angle of y and v projections in the X,Y
plane;
c_y and c_v = angle of y and v with their X,Y
projection, along Z dimension.
In the function graphs, controls L and M are for
parameter curves.
Some graphs have earlier versions with 3 axes coinciding
with the graph's, and a fourth projected upon those.
|
|
|
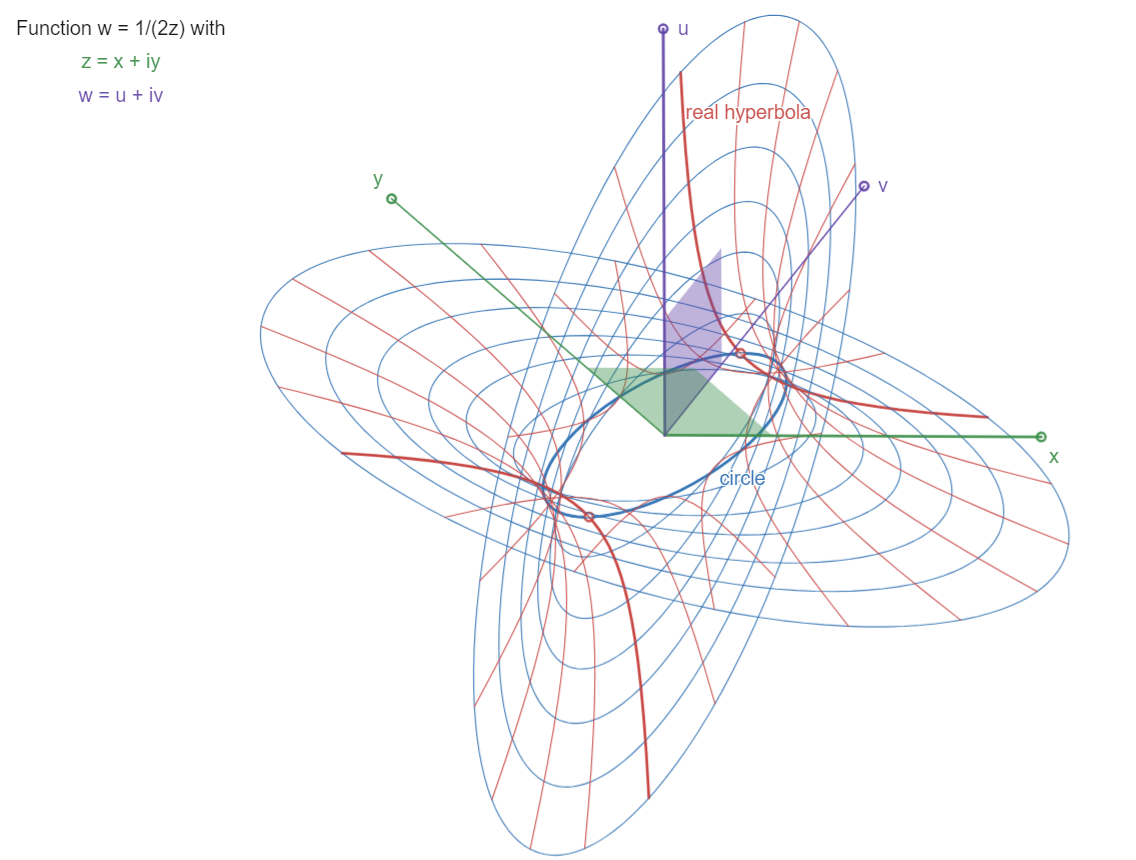
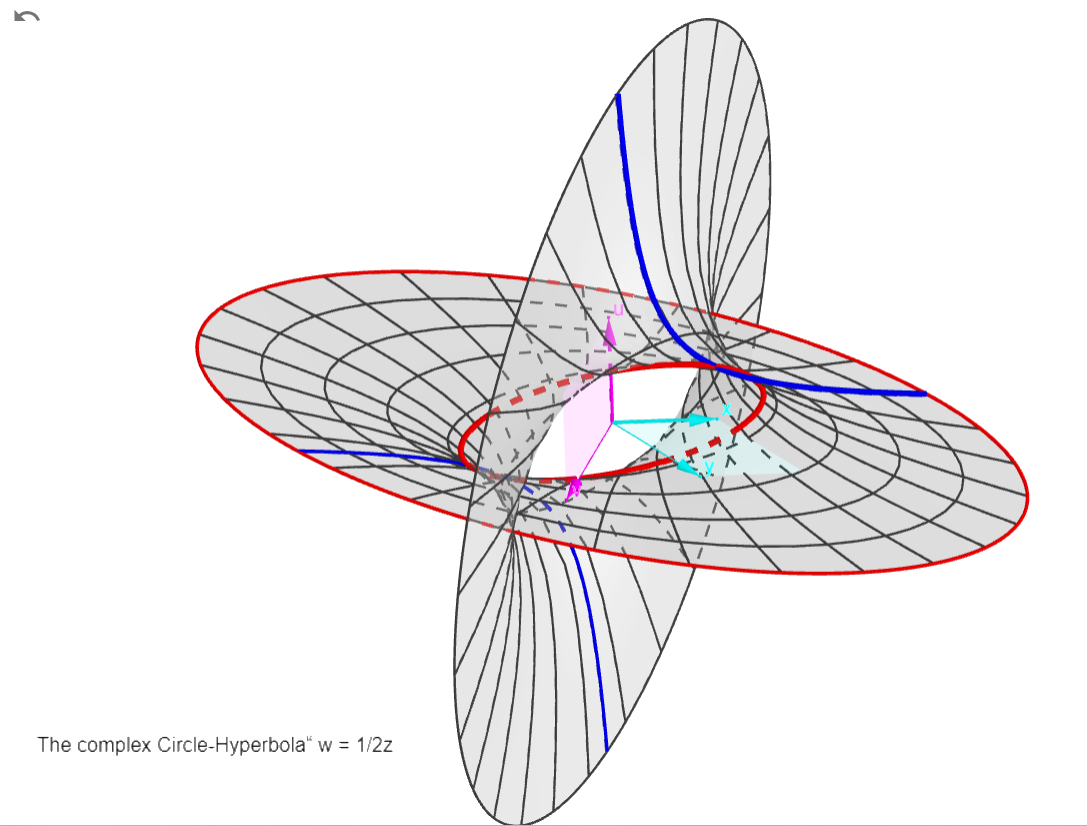
The Circle-Hyperbola:
w = 1 / 2z
There are two asymptotes: w=0 (the z plane) and z=0 (the
w plane, a pole: w->infinity), see the two "blades"
approaching the coordinate planes at infinity.
The red curves are hyperbolas (like the "real" one in
the x,u plane). The blue ones are circles (like the
central one, with radius 1 and real points
(x,u)=(0,+/-1)). That's why I call this function the
Circle-Hyperbola!
Circle and hyperbola are curves of the same surface in
complex space.
The complex function surfaces
ww+zz=1, ww-zz=1, ww+zz+1=0, w=1/z*sqrt(2)
represent a single surface, in different orientations
with "real curves" circle, hyperbola, imaginary circle,
and hyperbola respectively.
|
earlier version:
https://www.geogebra.org/calculator/kkp6d58s
|
|
|
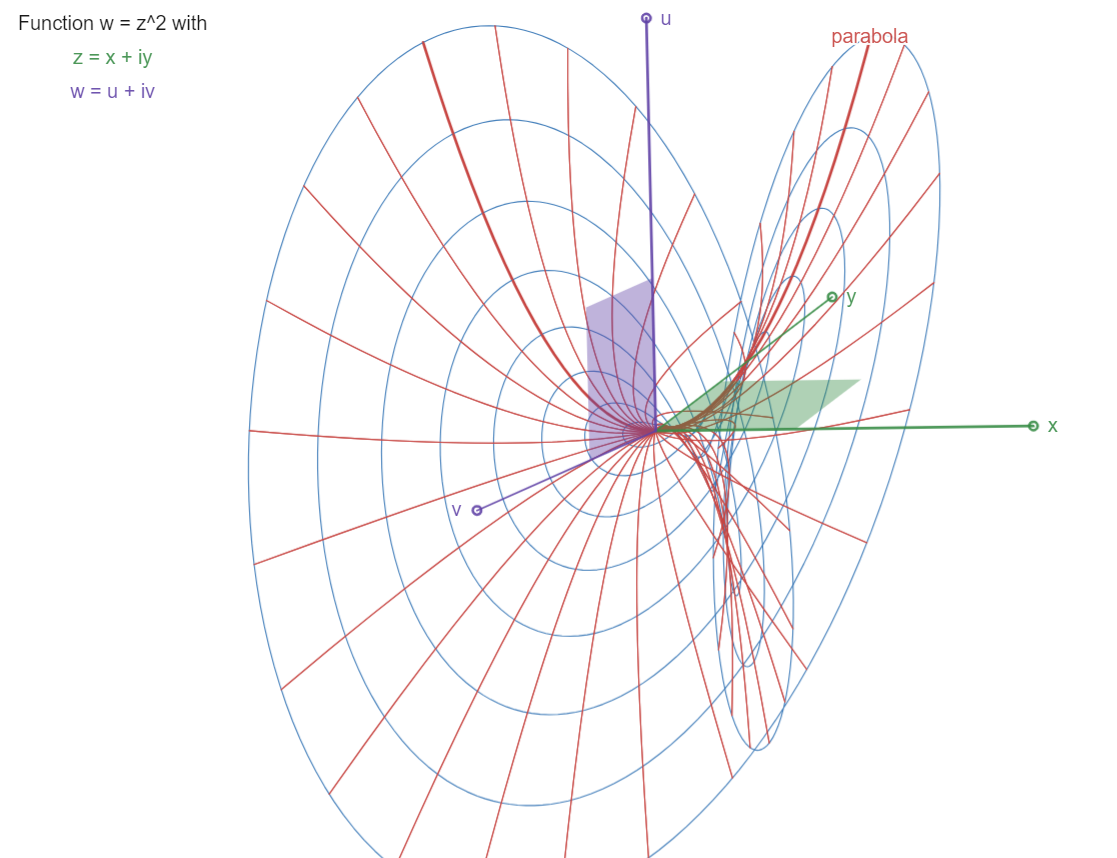
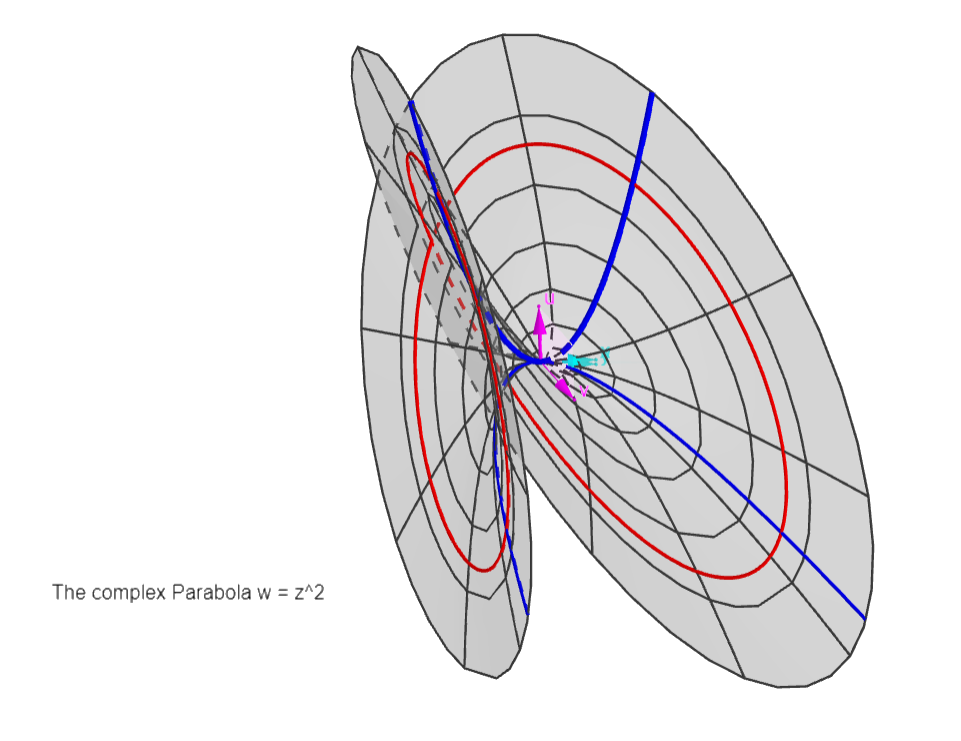
The Parabola:
w = z^2
A "4D paraboloid", with parabolas (in red, like the
"real" one in the x,u plane) rotating in complex space,
following their z-coordinates rotating in the z=x,y
plane.
|
Earlier
version:
https://www.geogebra.org/calculator/bw3xgauv
|
|
|
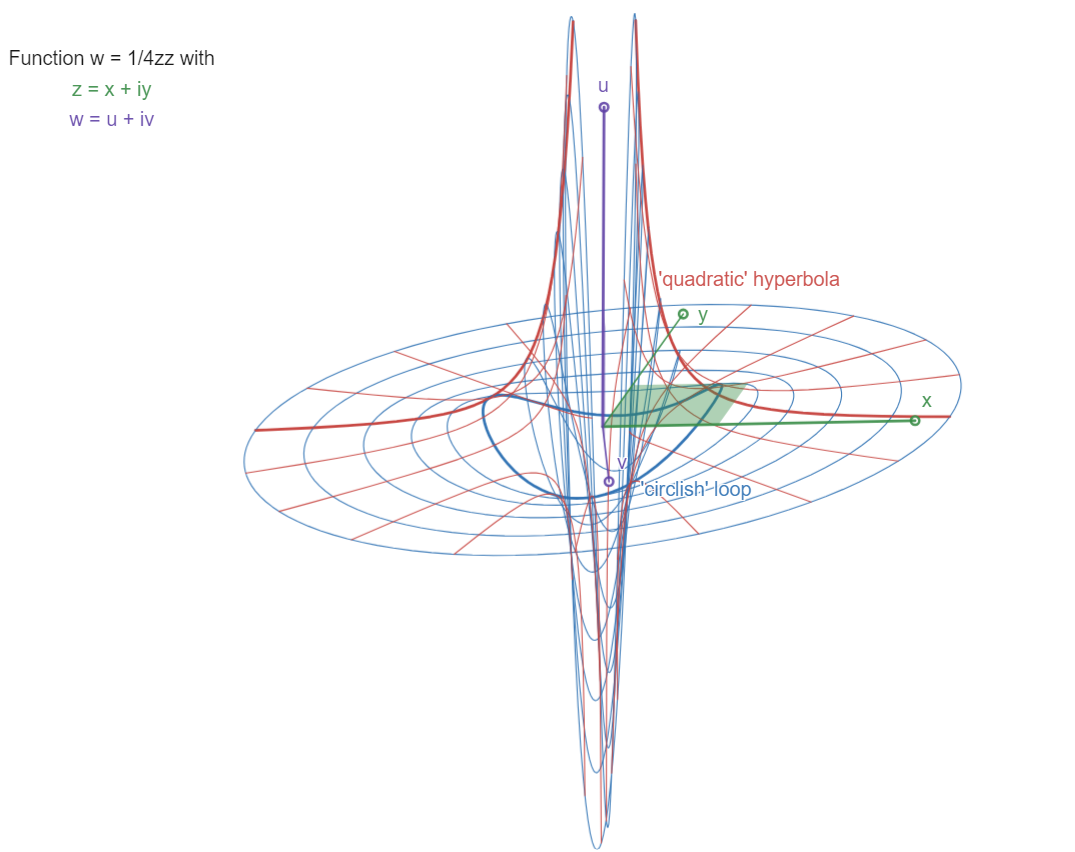
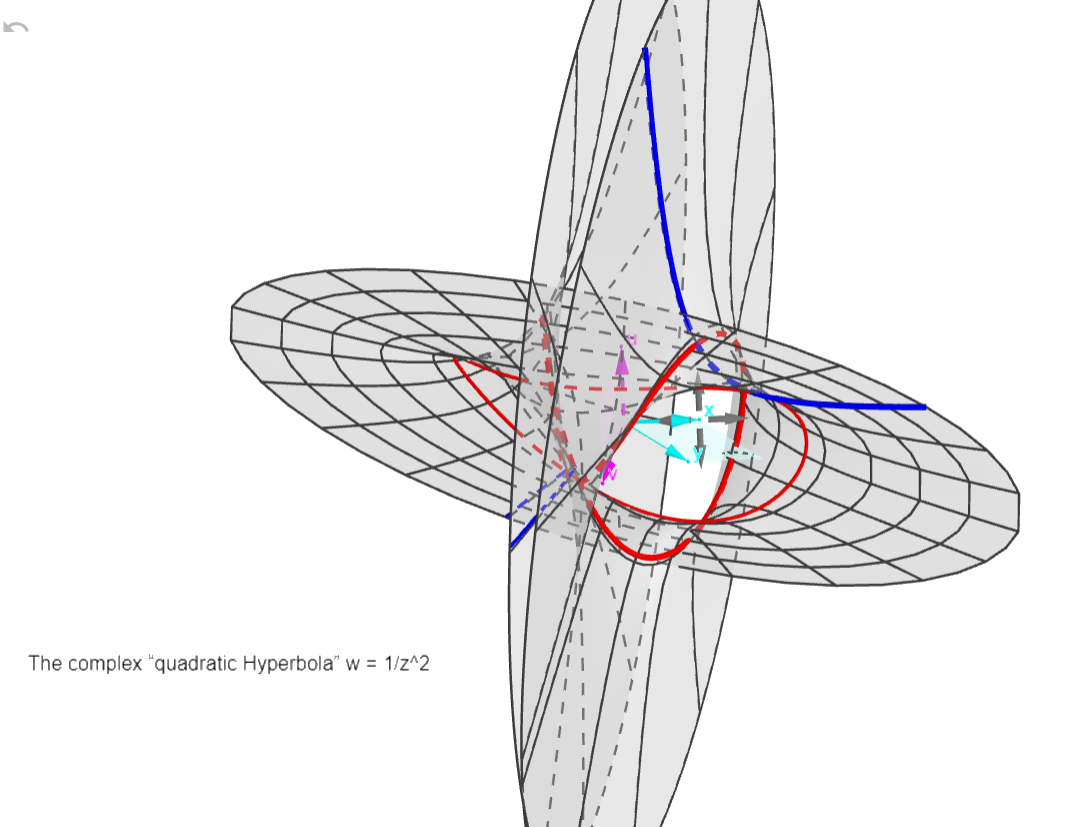
The "quadratic" Hyperbola:
w = 1 / 4z^2
There are two asymptotes: w=0 (the z plane) and z=0 (the
w plane, a pole: w->infinity, and yet a double one),
see the two "blades" approaching the coordinate planes
at infinity, the w-blade double (w rotates twice for one
z-rotation). The function is oriented with u,v plane
"frontal" so as to separate the double w-blade view.
Compare with the function w=1/2z, the "Circle-Hyperbola"
(its double name describing its parameter families).
Here we have "circlish" closed loops in blue, and
"quadratic hyperbola" twin curves in red.
|
Earlier
version:
https://www.geogebra.org/calculator/kb6sqtf9
|
|
|
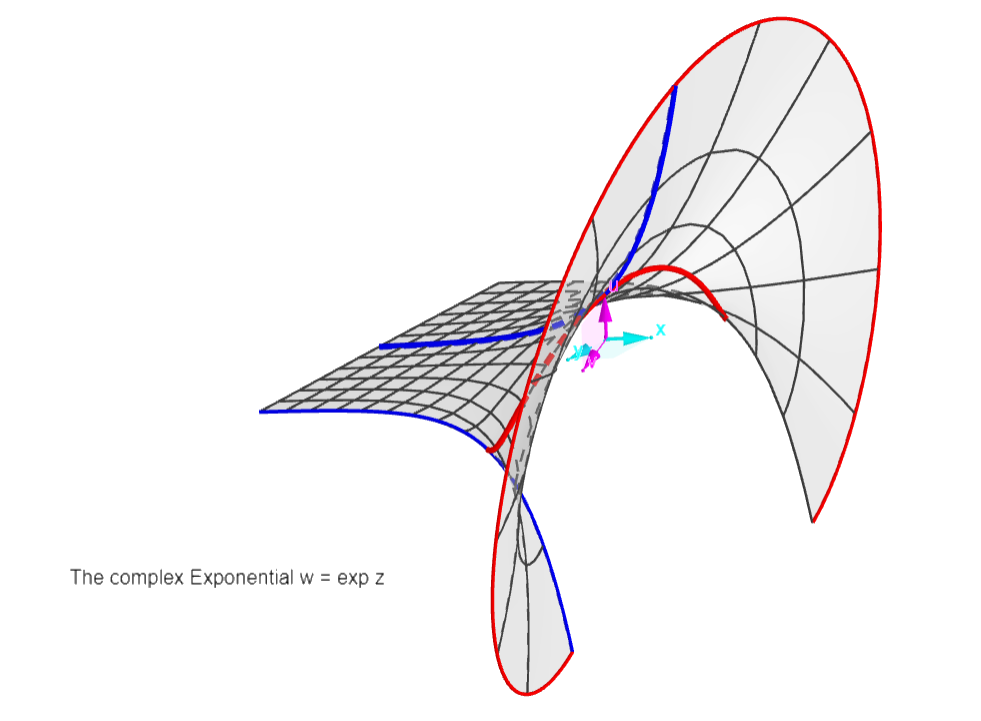
The Exponential:
w = exp z
Periodic function along y=Im(z) axis, period 2pi. One
period is shown, from -pi to +pi.
There is one asymptote: w=0 (the z plane), see the
"blade" approaching the coordinate plane at infinity to
the left.
The red curves are exponentials (like the "real" one in
the x,u plane), the blue ones are semi-sinusoids (like
the "semicosine" through the origin). That's why the
exponential and its reciprocal exp -z taken together
will form Sine functions (see graph of the Cosine)! The
asymptotes "left" and "right" will disappear, leaving
the reciprocal blades "left" and "right", separated by a
sine or cosine curve.
|
Earlier
version:
https://www.geogebra.org/calculator/zufs5s44
|

|
|
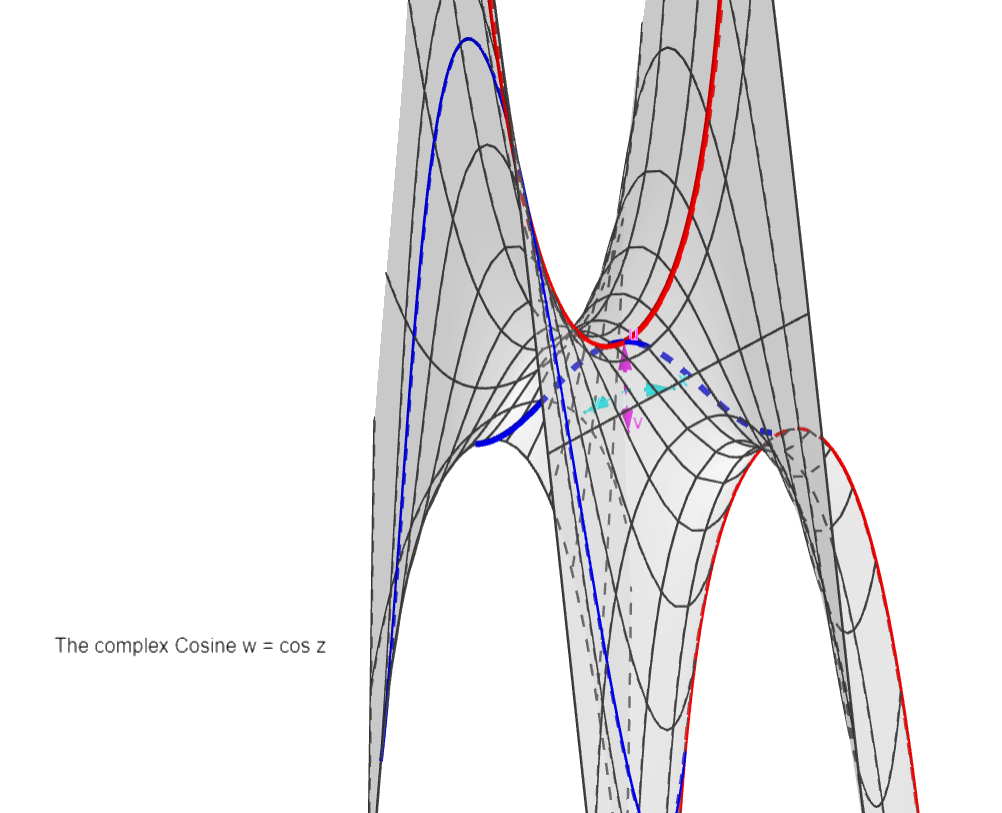
The Cosine:
w = cos z = 0.5*(exp z + exp -z)
Periodic function along x=Re(z) axis, period
2pi. One period is shown, from -pi to +pi.
The asymptotes of the exponential (see graph of that
function) and its inverse disappear, leaving two
opposite exponential blades.
The red curves are sinusoids, minimised at the real cos
curve (in the real plane x,u). The blue ones are
hyperbolic cosinoids, with periodic cosh and sinh
curves.
|
Earlier
versions:
https://www.geogebra.org/calculator/r8gxrmpf
https://www.geogebra.org/calculator/w8pmnpfu
|

|
|
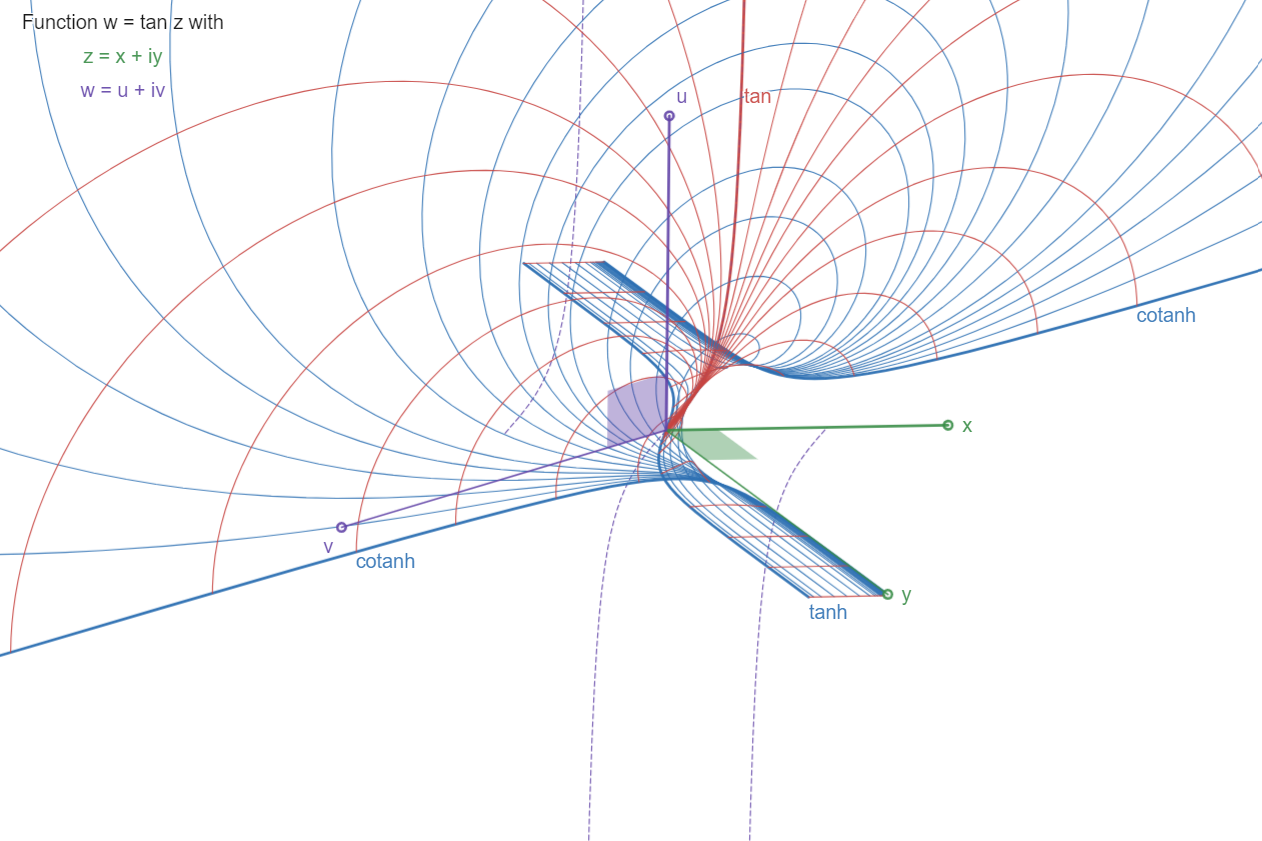
The Tangent:
w = tan z
Periodic function along x=Re(z) axis, period pi. A half
period is shown, from x=0 to +pi/2. The hatched curve
shows more of the real function u=tan x, in the x,u
plane.
The surface approaches asymptote plane x=pi/2 (parallel
to the u,v plane) by its "expanding" blade, which
contains the real curve
u=tan x,
and is limited by the curves
v=tanh y, for x=0, in the y,v plane, and
v=cotanh y, for x=pi/2, in the parallel plane.
|
|
|

|
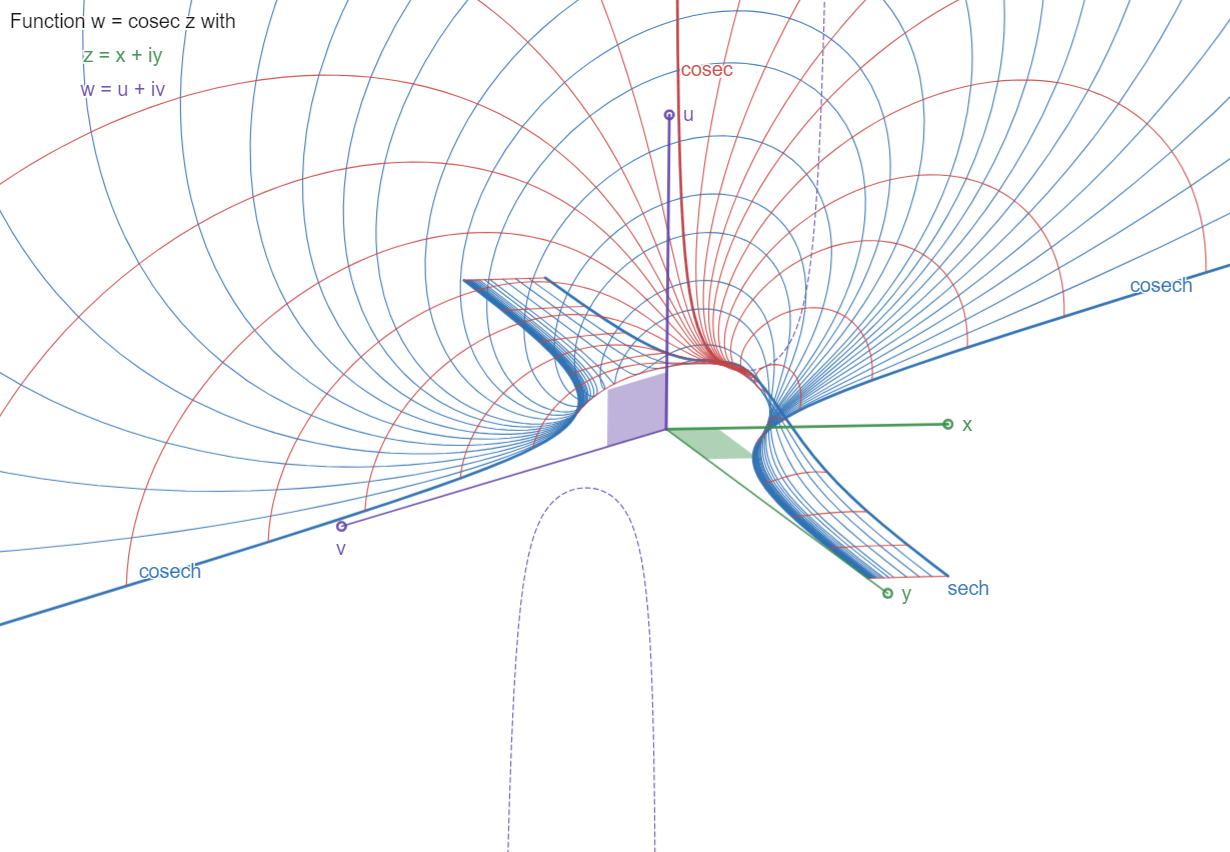
The Cosecant:
w = csc z
Periodic function along x=Re(z) axis, period 2pi. A
quarter of a period is shown, from x=0 to pi/2. The
hatched curve shows more of the real function u=csc x,
in the x,u plane.
The surface approaches asymptote plane x=0 (the u,v
plane) by its "expanding" blade, which contains
the real curve
u=cosec x
and is limited by the curves
u=sech y, for x=pi/2 parallel to the y,u plane, and
v=cosech y, for x=0 in the y,v plane.
|
|
|

|
|
|
|
|

