Elementaire begrippen i.v.m. reële functies

1. Inleiding

Deze webpagina behandelt de volgende onderwerpen:

· Grafieken van elementaire functies

· Transformaties van de grafiek y=f(x)

· Spiegelingen

Bij deze webpagina horen ook werkbladen.  Deze kan je hier vinden.

2. Grafieken van elementaire functies

In de applet hieronder kan je de grafieken van de verschillende basisfuncties laten tekenen. Dit kan je doen door zelf onderaan een waarde voor x in te geven of met de pijltjes de waarde van x te laten variëren. 

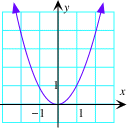
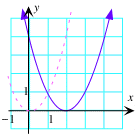
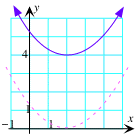
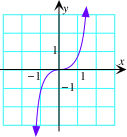
A. f(x)=x²	B. f(x)=x³
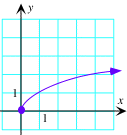
C. f(x)=x^(1/2)	D. f(x)=x^(1/3)
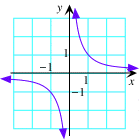
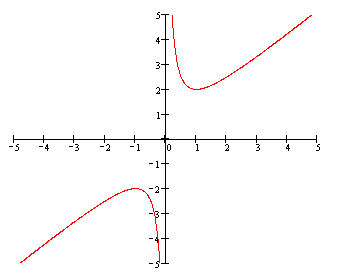
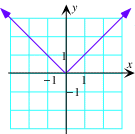
E. f(x)=1/x	F f(x)=|x|

3. Transformatie van de grafiek van y=f(x)

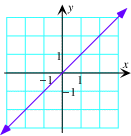
Laat ons eerst kijken naar de grafieken van sommige welgekende functies

f(x) = x

f(x) = x²

f(x) = x³

f(x)

=

1 x

f(x) = x^1/2

f(x) = |x|

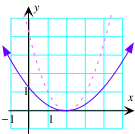
Maar wat over meer ingewikkelde functies. Bijvoorbeeld, hoe ziet f(x) = (x-3)² er uit?.  Merk op dat we f(x) = x² (een van de getekende functies hierboven) hebben genomen en x vervangen hebben door (x-3) om een nieuwe functie te bekomen. 

Wel, hier zijn enkele "hoofd" regels die ons vertellen wat het effect van deze operaties zijn.

a) "Verschuivings"-regels

Onderzoek de betekenis van de parameters a en b. 

Horizontale verschuiving: f(x) wordt f(x-a)

Verticale verschuiving: f(x) wordt f(x)+b

Overzicht

Regel	Voorbeeld
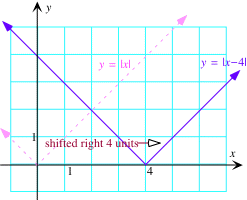
Horizontale verschuiving zij a een vast positief getal. x vervangen door x-a verschuift de grafiek a eenheden naar rechts. x vervangen door x+a verschuift de grafiek a eenheden naar links.	Hier is de grafiek van g(x) = |x4| . Deze is bekomen door de grafiek van f(x) = |x| vier eenheden naar rechts te verschuiven.
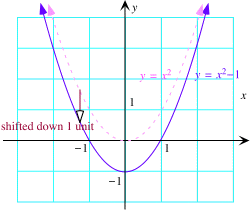
Verticale verschuiving zij b een vast positief getal. f(x) vervangen door f(x)+b verschuift de grafiek b eenheden naar boven. f(x) vervangen door f(x)-b verschuift de grafiek b eenheden naar beneden.	Hier is de grafiek van g(x) = x^2 1.  Deze is bekomen door de grafiek van f(x) = x^2  1 eenheid naar beneden te verschuiven.

Nu probeer zelfs een oefening te maken.

Voorbeeld 1 

Zij   f(x)

=

1 x + 1

.

Selecteer de juiste oplossing en druk op  "Check."

De grafiek van f(x) is bekomen door de grafiek van

1 x

door een verschuiving

naar boven naar beneden naar links naar rechts van 0 1 2 3 4

eenheden.

Nu, duid de juiste grafiek van de functie f aan.

---

De volgende oefening wordt verkregen door twee opeenvolgende translaties

Voorbeeld 2 

Zij  g(x) = (x2)^1/2 + 1. Selecteer de juiste optie en druk op  "Check."

De grafiek van g(x) wordt bekomen uit de grafiek van  x^1/2  door een verschuiving	naar boven naar beneden naar links naar rechts	met 2 eenheden, en
	naar boven naar beneden naar links naar rechts	1 eenheid.

Nu klik op de juiste grafiek van de functie f

Naast de verschuivingsregels, hebben we ook

b. "uitrekkings"-regel: f(x) wordt k^.f(x)

Onderzoek

Onderzoek de betekenis van de parameters k. 

Overzicht

Regel	Voorbeeld
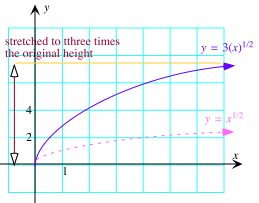
Verticale "uitrekking" Als g(x) = k^.f(x) met k positief dan: als k > 1, de grafiek van g is deze van f, maar uitgerokken in de y-richting (of vertikaal) met een factor k. Als 0 < k < 1, dan is de grafiek ingekrompen in de y-richting met een factor  1/k.	Hier is de grafiek van g(x) = 3(x)^1/2. Omdat k = 3 > 1, de grafiek wordt bekomen uit deze van  f(x) = x^1/2 uit te rekken in de y-richting met een factor k = 3.

Een voorbeeld

Voorbeeld 3 

Zij   g(x) =

1

3

x

+

1 x

.

Selecteer de juiste oplossing en druk op "Check."

De grafiek van g(x) wordt bekomen door de grafiek van

x

+

1

x

uit te rekken in te krimpen

met een factor

0 1 2 3 4

in de

x- y-

richting.

Als f(x)

=

x

+

1 x

dan is de grafiek van g:

---

Combinatie van verschuiving en uitrekking

Hier is een voorbeeld dat wordt bekomen door verschillende opeenvolgende transformaties

Voorbeeld 4 

Zij   g(x)   =

(x - 2)^2 3

+

4.

Selecteer de juiste oplossing

We starten met f(x) = x²,

Stap 1:  x vervangen   (x2), geeft (x2)².

Dit	verschuift de grafiek met rekt de grafiek uit met krimpt de grafiek in met 2 eenheden naar links 2 eenheden naar rechts 2 eenheden naar boven 2 eenheden naar beneden met een factor van twee eenheden

Stap 2: de laatste functie delen door 3 , geeft (x2)²/3.

Dit	verschuift de grafiek met rekt de grafiek uit met krimpt de grafiek in met 3 eenheden naar links 3 eenheden naar rechts 3 eenheden naar boven 3 eenheden naar beneden met een factor van drie eenheden

Stap 3: Tenslotte 4 optellen bij de laatste functie om de gegeven functie g te bekomen 

Dit	verschuift de grafiek met rekt de grafiek uit met krimpt de grafiek in met vier eenheden naar links vier eenheden naar rechts vier eenheden naar boven vier eenheden naar beneden met een factor van 4 eenheden

Hier zijn de grafieken die overeenkomen met deze stappen.

Originele functie
y = x²

Stap 1
y = (x2)²

Stap 2

y =	(x - 2)^2 3

Stap 3

y =

(x - 2)^2 3

+

4

---

Tenslotte kijken we naar spiegelingen

4. Spiegelingen

a) Spiegeling om de Y-as / Horizontale spiegeling: f(x) wordt f(-x)

Onderzoek de betekenis van f(x) wordt f(-x).

b) Spiegeling om de X-as / verticale spiegeling: f(x) wordt -f(x)

Onderzoek de betekenis van f(x) wordt -f(x). Volg hiervoor de instructies op je werkblad.

Overzicht

Regel	Voorbeeld
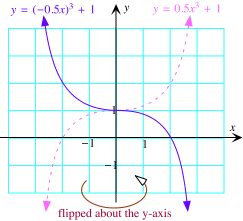
Spiegeling om de y-as / Horizontale spiegeling  x vervangen door  (x) spiegelt de grafiek t.o.v. de Y-as	Hier is de grafiek van  g(x) =0.125(-x)^3+1=-0.125x^3+1. Deze wordt bekomen door de grafiek van f(x) = 0.125x^3+1 te spiegelen rond de y-as.
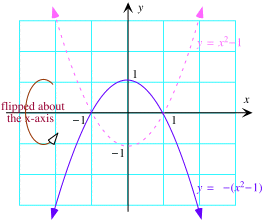
Spiegeling om de x-as / Vertikale spiegeling f(x) vervangen door  f(x) spiegelt de grafiek rond de x-as	Hier is de grafiek van  g(x) = (x^2 1). Deze werd bekomen door door grafiek van f(x) = x^2 1 te spiegelen rond de x-as

5. Oefeningen over dit onderwerp

---

Laatste Update 05/03/06door Karel Appeltans

Copyright © 1998 StefanWaner and Steven R. Costenoble