In een vierkant ABCD met zijde 2 liggen de punten P en Q op de diagonaal [BD] zodat |DP| = |QB| en |PQ| = 2. Hoe groot is de oppervlakte van driehoek ΔAPQ ?	A.   1
	B.
	C.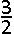
	D.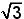
	E.   2

                     

Deze vraag (nr.8) werd gesteld op 9 maart 2022 tijdens de tweede ronde van de 21^ste Junior Wiskunde Olympiade (3^de en 4^de jaars).
55% gaf een juist antwword - 30% een fout antwoord - 15% gaf geen antwoord

Translation in   E N G L I S H

IN CONSTRUCTION	A.
	B.
	C.
	D.
	E.

Oplossing - Solution

1^ste manier :
De diagonaal heeft een lengte van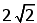 , de helft daarvan, is de hoogte van die driehoek met basis [PQ]. Vandaar dat zijn oppervlakte is .2. = .
2^de manier :
Verschuif het lijnstuk [PQ] to Q met B samenvalt. De oppervlakte van de driehoek zal hierdoor niet veranderen !. De driehoek is dan een driehoek met zijden 2 en ingesloten hoek van 45°. De oppervlakte is dus .2.2.sin 45° =