|
| A. 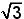 |
|---|---|
| B. 2 | |
| C. 3 | |
| D. | |
| E. 4 |
Deze vraag werd gesteld in januari 2022 tijdens de eerste ronde van de 37ste Wiskunde Olympiade (5de en 6de jaars).
20% juiste antwoorden - 45% foute antwoorden - 35% blanco's.
C en D werden evenveel gekozen
|
IN CONSTRUCTION |
A. |
| B. | |
| C. | |
| D. | |
| E. |
Neem de lengte van de zijden van de kleine zeshoek als eenheid.
Het overlappende driehoekje is dan een gelijkbenige driehoek met basishoeken van 30° en opstaanden zijden met lengte 1.
Het kwadraat van de basis wordt dan het antwoord.
Het driehoekje kan men verdelen in twee rechthoekige driehoeken
(30°-60°-90°) met schuine zijde 1 en rechthoekszijden en
en 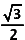 .
.
Die basis is het dubbel van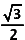 , dus
, dus 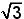 , zodat het antwoord (
, zodat het antwoord (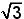 )² = 3 is.
)² = 3 is.
Het overlappende driehoekje is dan een gelijkbenige driehoek met basishoeken van 30° en opstaanden zijden met lengte 1.
Het kwadraat van de basis wordt dan het antwoord.
Het driehoekje kan men verdelen in twee rechthoekige driehoeken
(30°-60°-90°) met schuine zijde 1 en rechthoekszijden
 en
en 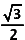 .
.Die basis is het dubbel van
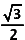 , dus
, dus 