Een rechthoekige driehoek heeft een hoek van 60°. De bissectrice (deellijn) uit die hoek verdeelt de driehoek in twee driehoeken waarvan de verhouding van de oppervlaktes gelijk is aan	A.   1
	B.
	C.
	D.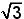
	E.   2

                 

Deze vraag (nr.14) werd gesteld in januari 2022 tijdens de eerste ronde van de 37^ste Wiskunde Olympiade (5^de en 6^de jaars).

Translation in   E N G L I S H

IN CONSTRUCTION	A.
	B.
	C.
	D.
	E.

Oplossing - Solution

De twee (kleinere) driehoeken hebben dezelfde hoogte. Hun oppervlakten verhouden zich dus als hun basissen. Wegens de bissectricestelling is dat precies gelijk aan de verhouding van de twee zijden van de hoek waaruit de bissectrice is getrokken. Dit is hier dus de verhouding van de schuine zijde tot de kortste rechthoekszijde (van de grote driehoek). In een 30°-60°-90° driehoek is dat precies 2 (heeft te maken met het feit dat sin 30° = cos 60° =  )