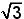Twee koorden van een cirkel met straal 1 hebben een lengte van en en hebben een eindpunt gemeen, zoals in de figuur. Wat is de hoek tussen de twee koorden ?	A.   60°
	B.   75°
	C.   90°
	D.   105°
	E.   120°

                     

De vraag werd gesteld aan de deelnemers van de tweede ronde van de 36^ste VWO (5^de en 6^de klassen)
(De tweede ronde is samengesteld uit ongeveer de 10% beste leerlingen van de eerste ronde)
Er waren 33% juiste antwoorden. Evenveel deelnemers dachten dat D het juiste antwoord was.
20% lieten de vraag onbeantwoord.

Translation in   E N G L I S H

IN CONSTRUCTION	A.
	B.
	C.
	D.
	E.

Oplossing - Solution

Een koorde van staat op een middelpuntshoek van 90°.
Immers, als je in een goniometrische cirkel de beeldpunten van 0° en 90° verbindt verkrijg je als koorde de diagonaal van een vierkant met zijde 1.
Een koorde van en 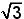staat op een middelpuntshoek van 120°.
Immers, als je in een goniometrische cirkel de beeldpunten van +60° en − 60° verbindt, verkrijg je een koorde die loodrecht staat op de x-as en dus lengte 2.sin60° = en 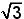heeft.
Beschouw de driehoek ABC met |AB| = en |AC| = en 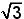, dan is wegens het verband tussen de omtrekshoeken en middelpuntshoeken die op dezelfde boog staan ACB = 45° (helft van 90°) en ABC=60° (helft van 120°). Bijgevolg is voor de gevraagde hoek CAB de grootte 180° − 45° − 60° = 75°