A B A' B' C D O
Een kwartcirkel CD met straal 1 en middelpunt O verdeelt men in 3 gelijke delen door middel van de punten A en B. Uit die punten laat men de loodlijnen AA' en BB' neer op de middellijn OC (zie figuur). De oppervlakte van het (gele) trapezium ABB'A' bedraagt 		A.   \(\boldsymbol{\frac {\sqrt 2} {4} }\)
B.   \(\boldsymbol{\frac {\sqrt 3} {6} }\)
C.   \(\boldsymbol{\frac {1} {4} }\)
D.   \(\boldsymbol{\frac {\pi} {8} }\)
E.   \(\boldsymbol{\frac {\pi} {12} }\)
               

[ vwo23-(2s11) - op net sinds 20.12.2022-()-3.10.2023 ]

Deze vraag (nr.11) werd gesteld op 27 februari 2008
tijdens de tweede ronde van de 23ste Wiskunde Olympiade (5de en 6de jaars).
48% van de deelnemers gaven een correct antwoord, 30% gaven geen antwoord.
De foute alternatieven kwamen alle vier ongeveer evenveel aan bod.
Translation in   E N G L I S H

IN CONSTRUCTION

Oplossing - Solution
Men kan de figuur beschouwen als een deel van een goniometrische cirkel waarbij A en B resp. de beeldpunten zijn van 60° en 30°. De hoogte van het trapezium is hier gelijk aan  cos 30° − cos 60° = \(\boldsymbol{\frac {\sqrt 3}{2} - \frac 12 = \frac{\sqrt 3\,-\,1}{2} }\)
De grote basis van het trapezium is sin 60° = 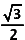v3/2
De kleine basis van het trapezium is sin 30° = 1/2
De oppervlakte van het trapezium ABB'A' = hoogte × gemiddelde van de twee basissen = \(\boldsymbol{\frac {\sqrt 3\, -\,1}{2} \cdot \frac 12\cdot\frac{\sqrt 3\,+\,1}{2} = \frac {3\,-\,1}{8} = \frac 14 }\)