De zijden van een gelijkzijdige driehoek ABC worden verdeeld in 2 stukken met lengte 1 en lengte x (x > 1). De verdeelpunten D, E, F zijn eveneens de hoekpunten van een gelijkzijdige driehoek. Hoe groot is x als de oppervlakte van ΔABC het dubbel is van de oppervlakte van ΔDEF?	A.   3
	B.   π
	C.   3,75
	D.   2 +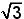
	E.   3 +

                     

[ vwo22-(2s13) - op net sinds 12.11.2022-(E) ]

Deze (13^de en moeilijke) vraag werd gesteld op 28 februari 2007, op de tweede ronde van de Wiskunde Olympiade (5de en 6de leerjaar)
Niet minder dan 65% van de deelnemers lieten de vraag open.
Ongeveer evenveel juiste als foute antwoorden (18%)

Translation in   E N G L I S H

IN CONSTRUCTION	A.
	B.
	C.
	D.
	E.

Oplossing - Solution

Noem de zijde van ΔABC   y. Dan is wegens de cosinusregel :
y² = 1 + x² − 2x.cos 60° = x² − x + 1.
De oppervlakteverhouding is dan \(\boldsymbol{(\frac {1+x} {y})^2=\frac{1\,+\,2x\,+\,x^2}{x^2\,-\,x\,+\,1} }\)
welke 2 moet zijn.
Vandaar dat dus   1 + 2x + x² = 2x² − 2x + 2  ⇔  0 = x² − 4x + 1
Deze vierkantsvergelijking heeft discriminant  D = 12  en oplossingen  ½(4 ±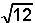 ) = 2 ± .
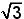Het antwoord is dus   2 +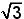   (ongeveer 3,7)