|
Als a en b gelijk zijn aan 6 klopt de gelijkheid \(\boldsymbol{\frac1a+\frac1b=\frac13}\). Als a en b verschillende natuurlijke getallen zijn, dan geldt dezelfde gelijkheid alleen als a + b gelijk is aan |
A. 3 |
|---|---|
| B. 6 | |
| C. 12 | |
| D. 16 | |
| E. 18 |
[ vwo21-(2s2) - op net sinds 20.12.2022-() ]
Deze vraag (nr.2) werd gesteld op 8 maart 2006
tijdens de tweede ronde van de
21ste Wiskunde Olympiade (5de en 6de jaars).
Deze vraag bleek een gemakkelijke vraag :
74% had het bij het rechte eind (15% four en 11% blanco)
|
IN CONSTRUCTION |
A. |
| B. | |
| C. | |
| D. | |
| E. |
Eén van beide breuken zal dan groter zijn dan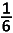 
(en de andere kleiner).
Bv. \(\boldsymbol{\frac1a > \frac16 }\) ⇔ a < 6
Bovendien moet ook a > 3 want anders is de som van 2 positieve getallen te groot en kan nooit gelijk zijn aan .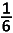
Blijft er nog twee mogelijkheden over :
a = 4 wat \(\boldsymbol{\frac14+\frac1b=\frac13 \Leftrightarrow \frac1b=\frac13-\frac14=\frac1{12} }\) waaruit b = 12 volgt.
a = 5 wat \(\boldsymbol{\frac15+\frac1b=\frac13 \Leftrightarrow \frac1b=\frac13-\frac15=\frac2{15} }\) wat echter geen stambreuk is. De enige mogelijkheid is dus a + b = 4 + 12 = 16
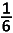(en de andere kleiner).Bv. \(\boldsymbol{\frac1a > \frac16 }\) ⇔ a < 6
Bovendien moet ook a > 3 want anders is de som van 2 positieve getallen te groot en kan nooit gelijk zijn aan
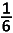.Blijft er nog twee mogelijkheden over :
a = 4 wat \(\boldsymbol{\frac14+\frac1b=\frac13 \Leftrightarrow \frac1b=\frac13-\frac14=\frac1{12} }\) waaruit b = 12 volgt.
a = 5 wat \(\boldsymbol{\frac15+\frac1b=\frac13 \Leftrightarrow \frac1b=\frac13-\frac15=\frac2{15} }\) wat echter geen stambreuk is. De enige mogelijkheid is dus a + b = 4 + 12 = 16
