|
De grootste waarde van sin x is 1. De grootste waarde van cos x is 1. Wat is de grootste waarde van sin²x + sin²x.cos²x + cos²x ? |
A. 1 |
|---|---|
| B. 2 | |
| C. 3 | |
D.  | |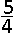
E.  |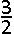
[ vwo21-(2s15) - op net sinds 18.12.2022-(E)- ]
Deze vraag (nr.15) werd gesteld op 8 maart 2006 tijdens de tweede ronde van de
21ste Wiskunde Olympiade (5de en 6de jaars).
52% gaf hierop een juist antwoord, 41% een fout en 7% een blanco antwoord
|
What is het largest value of sin²x + sin²x.cos²x + cos²x ? |
A. 1 |
| B. 2 | |
| C. 3 | |
| D. | |
| E. |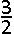
1ste manier :
Als twee positieve getallen a en b som 1 hebben (a+b=1), dan is hun product het grootst als ze gelijk zijn : immers hun product is y = a.b = a.(1-a) → een kwadratische functie ==> y is het grootste als a = (0+1)/2 = (=gemiddelde van de nulwaarden). Zo ook : sin²x . cos² x is het grootst als sin²x = cos²x d.i. als sinx=cosx of sinx=-cosx, m.a.w. x moet een veelvoud zijn van 45°.
In dat geval zijn sin²x = cos²x =
zodat sin²x . cos² x = 
.
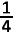Daar verder sin²x + cos² x = 1 is het antwoord dus 1 + = 1,25.
2de manier : (met de formule sin 2x = 2.sin x.cos x)
sin²x + sin²x.cos²x + cos²x
= 1 +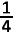.4. sin²x.cos²x
= 1 +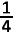.(2.sin x.cos x)²
= 1 +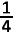.(sin 2x)²
Maximale waarde : 1 +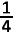.1 = 1 + 0,25 = 1,25
Als twee positieve getallen a en b som 1 hebben (a+b=1), dan is hun product het grootst als ze gelijk zijn : immers hun product is y = a.b = a.(1-a) → een kwadratische functie ==> y is het grootste als a = (0+1)/2 = (=gemiddelde van de nulwaarden). Zo ook : sin²x . cos² x is het grootst als sin²x = cos²x d.i. als sinx=cosx of sinx=-cosx, m.a.w. x moet een veelvoud zijn van 45°.
In dat geval zijn sin²x = cos²x =
zodat sin²x . cos² x = 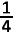.Daar verder sin²x + cos² x = 1 is het antwoord dus 1 + = 1,25.
2de manier : (met de formule sin 2x = 2.sin x.cos x)
sin²x + sin²x.cos²x + cos²x
= 1 +
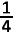.4. sin²x.cos²x= 1 +
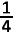.(2.sin x.cos x)²= 1 +
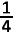.(sin 2x)²Maximale waarde : 1 +
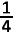.1 = 1 + 0,25 = 1,25
