|
Wat is het product van alle wortels van de vergelijking |x − 1|2 − 2 |x − 1| − 8 = 0 ? | A. −15 |
|---|---|
| B. − 8 | |
| C. −3 | |
| D. 5 | |
| E. 2 |
Deze vraag (nr.21) werd gesteld op 18 januari 2006 tijdens
de eerste ronde van de
21ste Wiskunde Olympiade (5de en 6de jaars).
Juiste, foute en blanco antwoorden waren "eerlijk" verdeeld :
Juist 31% - Fout 36% - Blanco 33%
|
IN CONSTRUCTION |
A. |
| B. | |
| C. | |
| D. | |
| E. |
1ste manier :
Stel |x − 1| = y.
We moeten dan de vkvgl. y² − 2y − 8 = 0 oplossen : wortels 4 en −2
a) |x − 1|= 4 ⇔ x − 1 = 4 ⇔ x − 1 = −4 ⇔ x = 5 ∨ x = −3
b) |x − 1|= −2 is een valse vergelijking.
Het antwoord is dus 5.(−3) = −15
2de manier :
Los de vergelijking apart op in ]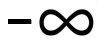
, 1] en [ 1,
[
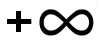a) in ]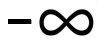,1 ] :
(x − 1)² − 2(−x + 1) − 8 = 0 ⇔ x² − 2x + 1 + 2x − 2 − 8 = 0
⇔ x² − 9 = 0 ⇔ x = 3 enkel −3 aanvaardbaar
b) in [ 1,[ :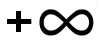
(x − 1)² − 2(x − 1) − 8 = 0 ⇔ x² − 2x + 1 − 2x + 2 - 8 = 0
⇔ x² − 4x − 5 = 0 ⇔ (x + 1)(x − 5) = 0 ⇔ x = −1 ∨ x = 5
enkel 5 aanvaardbaar
Het antwoord is hier ook (natuurlijk) (−3).5 = −15
Stel |x − 1| = y.
We moeten dan de vkvgl. y² − 2y − 8 = 0 oplossen : wortels 4 en −2
a) |x − 1|= 4 ⇔ x − 1 = 4 ⇔ x − 1 = −4 ⇔ x = 5 ∨ x = −3
b) |x − 1|= −2 is een valse vergelijking.
Het antwoord is dus 5.(−3) = −15
2de manier :
Los de vergelijking apart op in ]
, 1] en [ 1,[a) in ]
,1 ] :(x − 1)² − 2(−x + 1) − 8 = 0 ⇔ x² − 2x + 1 + 2x − 2 − 8 = 0
⇔ x² − 9 = 0 ⇔ x = 3 enkel −3 aanvaardbaar
b) in [ 1,
[ :(x − 1)² − 2(x − 1) − 8 = 0 ⇔ x² − 2x + 1 − 2x + 2 - 8 = 0
⇔ x² − 4x − 5 = 0 ⇔ (x + 1)(x − 5) = 0 ⇔ x = −1 ∨ x = 5
enkel 5 aanvaardbaar
Het antwoord is hier ook (natuurlijk) (−3).5 = −15