1,5 1 0,5 -0,5 -1 -1,5 -2 -1 1 2 3 P x gricha - v8356 - 16.7.2022
In het punt  P ( 1, 1/2 ) aan de parabool met vgl.  y = 1 − 1/2 x² tekent men de raaklijn.
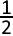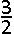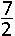Deze raaklijn gaat door het punt met coördinaat 		A.   ( 3,  )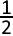
B.   ( 3, −  )
C.   ( 3, −1 )
D.   ( 3, −  )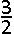
E.   ( 3, −  )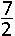
                 

[ 5-8356 - op net sinds 23.4.2018-(E)-3.11.2023 ]

Translation in   E N G L I S H

The tangent is drawn at the point   P ( 1, ½ )   on the parabola   y = 1 − ½ x².
This tangent line passes through the point 		A.  A ( 3, )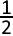
B.  B ( 3,− )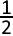
C.  C ( 3,−1)
D.  D ( 3,− )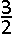
E.  E ( 3,− )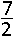

Oplossing - Solution

De afgeleide van   y   is   y' = −x.
De richtingscoëfficiënt van de raaklijn in P(1,½) is dus −1.
De vergelijking van de rechte in   P(1,½)   is bijgevolg
y − ½ = −1(x − 1) = −x + 1 ⇔ y = −x + 1,5
Voor   x = 3   levert dat de waarde   y = −3 + 1,5 = −1,5