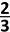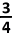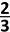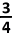De grafiek van y2 = x2 − x4 kan gezien worden als de ideale vorm voor het symbool oneindig.
Deze past precies in een rechthoek die de grafiek in zes punten raakt (zie figuur).
Welk deel van die rechthoek wordt door het (blauwe) symbool ingenomen ?
| A.  |
|---|
B. 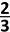 |
C. 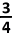 |
D. 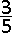 |
E. 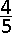 |
[ 6-8166 - op net sinds 3.1.2018-()-19.12.2023 ]
Translation in E N G L I S H
IN CONSTRUCTION
ratio blue/rectangle
|
|---|
Oplossing - Solution
De nulwaarden van x² − x⁴ = x²(1 − x²) zijn de getallen −1, 0 en +1.
De langste afmeting van de rechthoek is dus 2.
Voor de andere afmeting moeten we eerst het maximum bepalen van
de functie \(y=x\sqrt{1-x^2}\). Dit doen we m.b.v. de afgeleide :
\(D\;y=D\;\left(x\sqrt{1-x^2}\right)=\sqrt{1-x^2}+x.\frac{1\left(-2x\right)}{2\sqrt{1-x^2}}=\frac{1-x^2-x^2}{\sqrt{1-x^2}}=\frac{1-2x^2}{\sqrt{1-x^2}}
\)
De nulwaarden volgen uit 1 − 2x² = 0 ⇔ x² = ½ ⇔ x = . . .
zodat de (pos.) corresponderende y-waarde is \(\sqrt{\frac{1}{2}}.\sqrt{1-\frac{1}{2}}=\sqrt{\frac{1}{2}}.\sqrt{\frac{1}{2}}=\frac{1}{2}\).
De andere afmeting van de rechthoek is dus 2.½= 1.
De oppervlakte van die rechthoek is bijgevolg 1.2 = 2
De oppervlakte van het blauwe gebied berekenen we met een
bepaalde integraal. Rekening houdend met het feit dat zowel de x-as
als de y-as symmetrie-assen zijn, wordt die oppervlakte gegeven door
\(4\int_{0}^{1}ydx=4\int_{0}^{1}{x\sqrt{1-x^2}dx}=-2\int_{0}^{1}{\sqrt{1-x^2}d\left(1-x^2\right)}\\
=-2\int_0^1(1-x^2)^\frac12\:d(1-x^2)=-2\left[\frac{(1-x^2)^\frac32}{\frac32}\right]_0^1\\
=-\frac43\left[(1-x^2)^\frac32\right]_0^1=-\frac43[0-1]=\frac43\)
De gevraagde verhouding is dus \( \frac{4}{3}:2=\frac{2}{3}\)