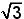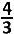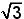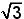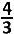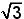Wegens de snijpunten (− 4, 0) en ( 4, 0 ) op de x-as,
zijn er twee nulwaarden nl. ±4 en heeft de parabool een vergelijking van de vorm y = a(x² − 16).
Daar ook ( 0, 4 ) een punt is van de parabool moet 4 = a.(0 − 16) zodat
a = −
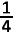
.
De vergelijking van de parabool is dus y = −
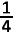
(x² − 16) en elk punt van de parabool kan voorgesteld worden door het koppel (x, −
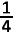
(x² − 16) )
De oppervlakte S van de rechthoek is dan S = 2.x.( −
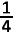
)(x² − 16)
= −
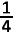
(x³ − 16x).
Om een extremum te vinden van deze derdegraadsuitdrukking gaan we S afleiden :
D S =
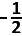
(3x² − 16) met nulwaarden \(\pm\sqrt{\frac{16}{3}}=\pm\sqrt{\frac{48}{9}}=\pm\sqrt{\frac{163}{9}}=\pm\frac{4}{3}\sqrt3\approx2,3\)
Omdat rond \(x=\frac43\sqrt3\) de afgeleide "+ 0 −" is zal S het gedrag ↗
max ↘
vertonen zodat we met zekerheid kunnen zeggen dat \(\small x=\frac43\sqrt3\) het antwoord is.