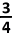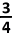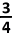Het schaadt de algemeenheid niet als we voor de zijde van het vierkant 2 nemen.
1ste manier :
=\cot2\beta
=\frac{\cos&space;2\beta}{\sin&space;2\beta}
=\frac{\cos^2\beta-\sin^2\beta}{2.\sin\beta.\cos\beta}\\
=\frac{\left(\frac{2}{\sqrt5}\right)^2-\left(\frac{1}{\sqrt5}\right)^2}{2.\frac{1}{\sqrt5}.\frac{2}{\sqrt5}}
=\frac{4-1}{4}=\frac34 "\\\tan\alpha=\tan(90^\circ-2\beta)=\cot2\beta=\frac{\cos 2\beta}{\sin 2\beta}=\frac{\cos^2\beta-\sin^2\beta}{2.\sin\beta.\cos\beta}\\=\frac{\left(\frac{2}{\sqrt5}\right)^2-\left(\frac{1}{\sqrt5}\right)^2}{2.\frac{1}{\sqrt5}.\frac{2}{\sqrt5}}=\frac{4-1}{4}=\frac34")
2de manier :
=\cot2\beta=\frac{1}{\tan&space;2\beta}=
\frac{1-\tan^2\beta}{2\tan\beta}=\frac{1-\frac14}{2.\frac12}=
\frac34 "\\\tan\alpha=\tan(90^\circ-2\beta)=\cot2\beta=\frac{1}{\tan 2\beta}
=\frac{1-\tan^2\beta}{2\tan\beta}=\frac{1-\frac14}{2.\frac12}=\frac34")
3de manier :
Als je nog één lijnstuk trekt zie je dat je dat drie van de vier delen van het vierkant
bestaat uit rechthoekige driehoeken : twee met rechthoekszijden 1 en 2 (en dus schuine zijde
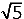
) en één gelijkbenige rechthoekige driehoek
met rechthoekszijden 1 (en dus schuine zijde
).
Door toepassing van de cosinusregel in de 'binnenste' driehoek verkrijgen we dan :
\((\sqrt2)^2=(\sqrt5)^2+(\sqrt5)^2-2.\sqrt5.\sqrt5.\cos\alpha \;\;⇔\;\; 2 = 5 + 5 − 10.\cos\alpha\\ ⇔ −8= −10.\cos\alpha \;\;⇔\;\; \cos\alpha = \frac{-8}{-10}=\frac45\\
1+\tan^2\alpha=\frac{1}{\cos^2\alpha} \;\;⇔\;\;1+\tan^2\alpha=\frac{25}{16}\;\;⇔\;\;\tan^2\alpha=\frac{9}{16} \)
Hieruit volgt dus direct de waarde van α
