een bol ingeschreven.
De verhouding van de
oppervlakte van de bol
tot de oppervlakte
van de kubus bedraagt
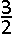
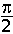
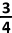 π
π
|
Een kubus is in een bol ingeschreven. De verhouding van de oppervlakte van de bol tot de oppervlakte van de kubus bedraagt | A. 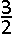 |
|---|---|
| B. 2 | |
C. 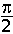 | |
D. 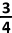 π π | |
E.  |
[ 4-4612 - op net sinds 24.2.15-()-27.10.2023 ]
| IN CONSTRUCTION | A. |
|---|---|
| B. | |
| C. | |
| D. | |
| E. |
