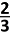
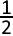
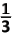
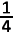
Een muntstuk is aan beide kanten rood geverfd. Een ander muntstuk is aan de ene kant rood en aan de andere kant blauw geverfd. [ De randen zijn wit geverfd ]. Zonder te kijken leg je de twee munten boven elkaar op tafel. Nu blijkt de bovenkant (van het stapeltje) rood te zijn.
Wat is de kans dat de kant die de tafel raakt blauw is ? 		A.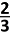  
B.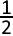  
C.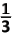  
D.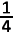  
E.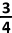  
                 

[ 6-3147 - op net sinds 2.2.15-()-25.10.2023 ]

Translation in   E N G L I S H

IN CONSTRUCTION A.  
B.  
C.  
D.  
E.  

Oplossing - Solution

We noemen de kanten van het eerste muntstuk : R1 en R2
We noemen de kanten van het tweede muntstuk : R en B
Er zijn dan acht even waarschijnlijke stapeltjes te maken
( 8 = 2x2x2, 2 mog. voor eerste muntstuk, 2 mog. voor tweede muntstuk, 2 mog. voor boven of onder) :
R1 R1   R2 R2   R   B      R   B →bovenkant
R   B     R   B     R1 R1   R2 R2 →tafelkant
Je ziet dus dat in de 6 gevallen waarbij rood boven ligt, 4 keer ook rood de tafel raakt. De kans is dus 4 op 6 of 2 op 3