De parabool met vergelijking y = − x2 + 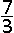 x + 2  snijdt de (pos.) x-as in het punt A en de y-as in het punt B.
Wat is de oppervlakte van OAB ? 		A. 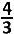  4/3
B.   2
C.   3
D.   4
E.   6
                 

[ 4-0186 - op net sinds 23.3.2020-(E)-20.10.2023 ]

Translation in   E N G L I S H

IN CONSTRUCTION
 A.  
B.  
C.  
D.  
E.  

Oplossing - Solution

Snijpunt met de y-as : (stel x=0) → (0,2)
Snijpunten met de x-as vind je door de nulwaarden te zoeken van −x² + 7/3x + 2 = 0 ⇔ −3x² + 7x + 6 = 0
Daar f(3)=0 (want -3.9 + 21 + 6 = 0) wordt de positieve x-as gesneden in (3,0)
[ daar −3x² + 7x + 6 = (x − 3)(−3x − 2) zie je dat de andere nulwaarde negatief is ]
De rechthoekszijden van ΔOAB hebben dus een lengte van 2 en 3 zodat de oppervlakte van de driehoek gelijk is aan ½.2.3 = . . .
GWB